I have added a stat that is called xG chain and xG build up that was created by Ted Knutson and Thom Lawrence for Statsbomb services. Mine might be a bit different but I have tried to follow the same general guidelines laid out in their introductory post on Statsbomb Services.
This is cool and helpful but it misses a lot of passes that don't lead to shots so I wanted to see about figuring out a way to include those. I really liked the way that Nils Mackay went about analyzing the problem and decided to use that as the starting point for my model. Mackay has gone even further in refining his model but for now I focused on making this simple for my first attempt.
What I am setting out to measure is the value added (xG in this case) between the starting point of a pass and where the pass ends.
The sporting logic behind this is that to be able to win you must score goals. Your team is better able to score goals the closer they are able to take shots to the opponents goal. Getting closer to the opponents goal through passing increases the likely hood of taking high quality shots. This last part is what I am looking to attempt to measure.
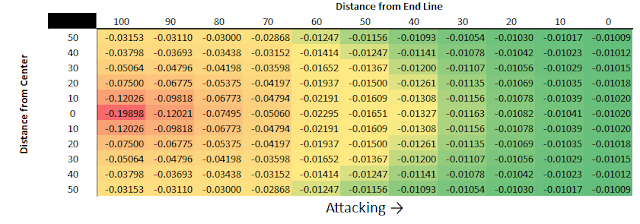
To accomplish this I use a very simple xG model to assign a value for every position on the pitch.
The equation for the xG model is this:
(1-(1/(1+((e^(-1.56335793278499+(Distance from Center*0.0000564550258161941)+ (Square Root (Distance from Endline^2+Distance from Center^2))*-0.0693321731182481)))))))
Essentialy it looks at how far you are from the center of the pitch (Closer to the Center is better) and how far you are from the center of the goal (Closer to the Center is better).
Here is what the values for areas of the field look like up and down the pitch:
So for example a completed pass starts at the point (60,10) and ends at the point (40,0). The end value is 0.01591 minus starting value of 0.00608 would give a simple value added of this pass of 0.00983. I have also made the decision to give a completed pass a bonus of 0.003 (the reasoning is that keeping possession to be able to continue to attack is valuable and this seems like a reasonable amount to assign, I am open to changing this) and if it starts and stays within the attacking final third an additional 0.015 is added (same reasoning as above but the attacking final third is even more important). So the total value added with this pass is 0.01283.
For an incomplete pass a player is penalized for the value to the opponent taking over at the end point of the pass. This is what the value of the pitch look like:
An example again, lets say that again we try to pass from the point (60,10) and ends at the point (40,0) but is intercepted. The value for this pass would be -0.01327, -0.00327 for the opponent taking over and -0.01 for losing possession.
These calculations are done for every pass attempt in the game.
I have gone back and done this for all of the games in the 2017-18 season thus far and added this stat to the Tableau database under the passing tab.
Also here are the top 25 in raw Value Added from the Premier League through the first 3 weeks:
Passing Progression Value Added (raw total) for the first 3 weeks of Premier League top 25 pic.twitter.com/f7FZQbGnlb— Scott Willis (@oh_that_crab) September 7, 2017
